Tech-X FPS
5•24•2019
space
charge
limited
emission
in
Presented by
Andrew Chap
*Auto-zoom is disabled because it doesn't work well with Plotly. Please set your browser to full-screen and zoom in or out until the slides take up the entire page.
I. introduction
OUTLINE
I. introduction
II. electrostatics
III. electromagnetics
IV. temporal response
V. applications
I
INTRODUCTION
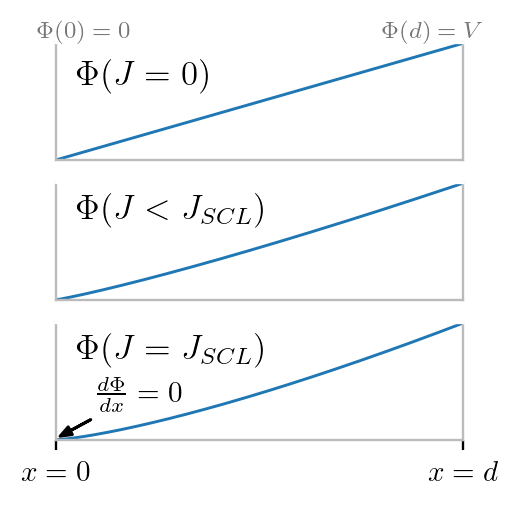
The 1-D Child-Langmuir Law
Two boundaries:
- Separated by distance $d$ (domain length)
- Voltage bias $V$
- Particles injected at left boundary with $v_0 = 0$
$J_\mathrm{SCL}$ is the maximum current that can cross the domain due to Space-Charge-Limiting:
$$J_\mathrm{SCL} = \frac{4}{9}\epsilon_0\sqrt{\frac{2 e}{m}}\frac{V^\frac{3}{2}}{d^2}$$
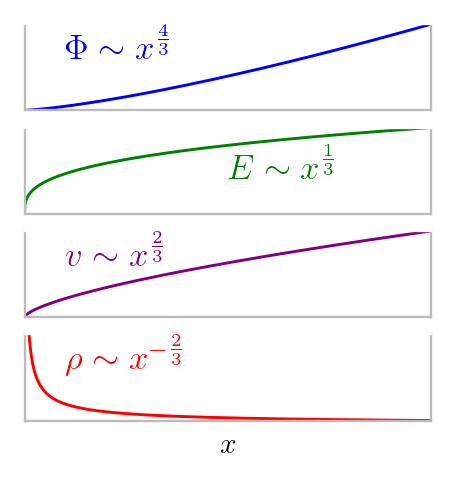
$\Phi$, $E$, $v$, and $\rho$
Generalize: $d\rightarrow x$, $V \rightarrow \Phi(x)$
$ \color{blue}{\Phi(x)} = \left(\frac{9}{4} \frac{J_\mathrm{SCL}}{\epsilon_0}\right)^{\frac{2}{3}} \left(\frac{m}{2e} \right)^{\frac{1}{3}} \color{blue}{x^\frac{4}{3}}$
$ \color{green}{E(x)} = \frac{d\color{blue}{\Phi(x)}}{dx} = \frac{4}{3}\left(\frac{9}{4} \frac{J_\mathrm{SCL}}{\epsilon_0}\right)^{\frac{2}{3}} \left(\frac{m}{2e} \right)^{\frac{1}{3}} \color{green}{x^\frac{1}{3}}$
$ \color{purple}{v(x)} = \sqrt{\frac{2 e\color{blue}{\Phi(x)}}{m}} = \left(\frac{9}{2} \frac{e J_\mathrm{SCL}}{m\epsilon_0}\right)^{\frac{1}{3}}\color{purple}{x^\frac{2}{3}}$
$ \color{red}{\rho(x)} = \frac{J_\mathrm{SCL}}{\color{purple}{v(x)}} = \left(\frac{2}{9} \frac{m \epsilon_0 J^2_\mathrm{SCL}}{e}\right)^{\frac{1}{3}}\color{red}{x^{-\frac{2}{3}}}$
Simulating Space-Charge-Limited (SCL) Emission in 1D
Because the equations for SCL flow are self-similar, we can simulate SCL emission on the left boundary without any information from the right boundary
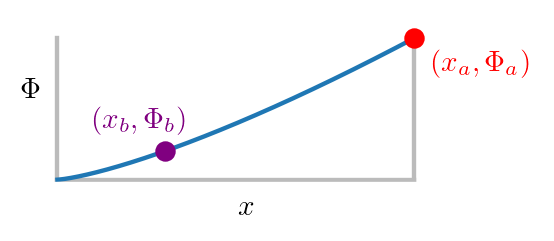 $$ \color{red}{J_\mathrm{SCL}\left(x_a,\Phi_a\right)} = \color{purple}{J_\mathrm{SCL}\left(x_b,\Phi_b\right)}$$
$$ \color{red}{J_\mathrm{SCL}\left(x_a,\Phi_a\right)} = \color{purple}{J_\mathrm{SCL}\left(x_b,\Phi_b\right)}$$

Plasma,
Complex Geometry
etc...
$$\color{purple}{\left(\Delta x,\Phi(\Delta x)\right)}$$
To simulate the local emission at the left boundary, we can calculate
$$J_\mathrm{emit} = J_\mathrm{SCL}(\Delta x, \Phi(\Delta x))$$
We can use $\Phi(\Delta x) = E_0\Delta x$ so that our emitted current is:
$$J_\mathrm{emit} = \frac{4}{9}\epsilon_0\sqrt{\frac{2 e}{m}}\frac{E_0^\frac{3}{2}}{\sqrt{\Delta x}}$$
where $E_0 = E(x=0)$ is the surface electric field and we take $\Phi(x=0)=0$.
Simulating Space-Charge-Limited (SCL) Emission in 1D
So we have: $J_\mathrm{emit} \sim \dfrac{E_0^\frac{3}{2}}{\sqrt{\Delta x}}$
Looks strange... because
- In space-charge-limited emission, $E_0$ should be zero
- Our emitted current goes as $\Delta x^{-\frac{1}{2}}$
But...
- Because of finite differencing, we will never get $E_0 = 0$, because $E_0 = \frac{\Phi(\Delta x) - \Phi(0)}{\Delta x}$ with $\Phi \sim x^\frac{4}{3}$
- Since $E \sim x^\frac{1}{3}$, we have $E^\frac{3}{2} x^{-\frac{1}{2}} \sim 1$
II
ELECTROSTATICS
Results: $J_\mathrm{SCL}$ vs spatial resolution
Test Problem:
$V = 1\,\mathrm{Volt}$, $L = 1\,\mathrm{meter}$
Electrons emitted from left boundary
Steady-state results from calculating $J_\mathrm{SCL}$ from the self-consistent electric field at the left surface
$$\mathrm{Error}\left[J_\mathrm{SCL}\right]\sim \Delta x^\frac{2}{3}$$
Results: $J_\mathrm{SCL}$ vs spatial resolution
Test Problem:
$V = 1\,\mathrm{Volt}$, $L = 1\,\mathrm{meter}$
Electrons emitted from left boundary
Steady-state results from calculating $J_\mathrm{SCL}$ from the self-consistent electric field at the left surface
$$\mathrm{Error}\left[J_\mathrm{SCL}\right]\sim \Delta x^\frac{2}{3}$$
Results: $J_\mathrm{SCL}$ vs spatial resolution
Test Problem:
$V = 1\,\mathrm{Volt}$, $L = 1\,\mathrm{meter}$
Electrons emitted from left boundary
Steady-state results from calculating $J_\mathrm{SCL}$ from the self-consistent electric field at the left surface
$$\mathrm{Error}\left[J_\mathrm{SCL}\right]\sim \Delta x^\frac{2}{3}$$
What about returning current?
Same test as before except electrons reflected at right boundary
• Theoretical result: $\left[J_\mathrm{SCL}\right]_\mathrm{two-way} = \frac{1}{2} \left[J_\mathrm{SCL}\right]_\mathrm{one-way}$ since reflected particles create twice the space charge
• In numerical experiments, $\left[J_\mathrm{SCL}\right]_\mathrm{two-way} \lt \frac{1}{2} \left[J_\mathrm{SCL}\right]_\mathrm{one-way}$ because not all particles have exactly the energy needed to return to the cathode, some get trapped and create a virtual cathode that reduces $J_\mathrm{SCL}$
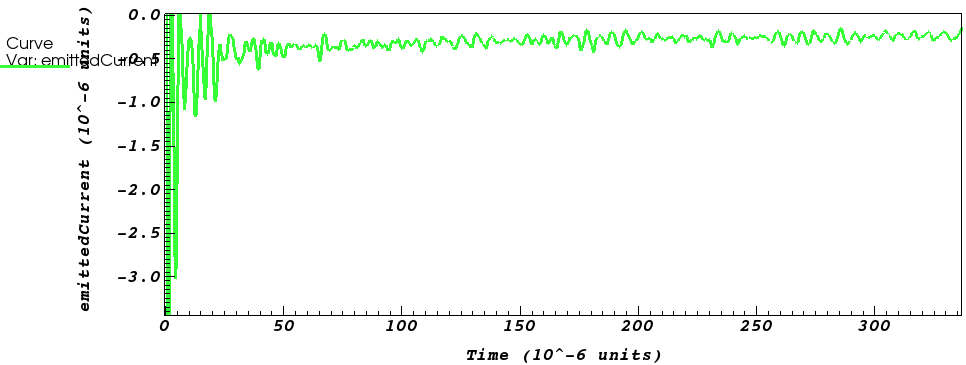
$J_\mathrm{SCL}(t)$
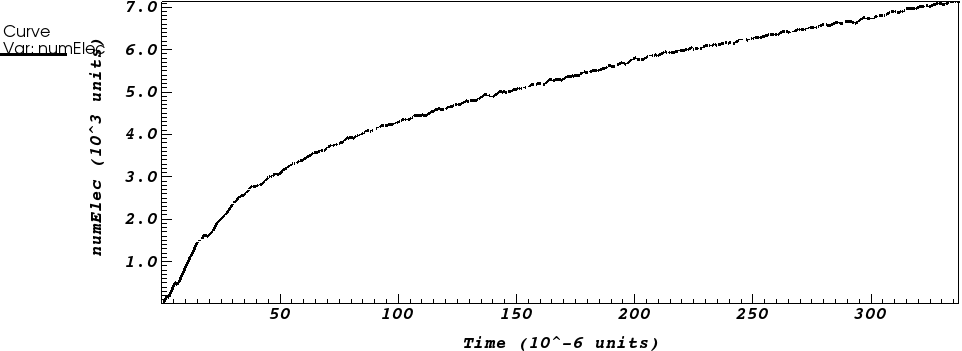
$N_\mathrm{electrons}(t)$
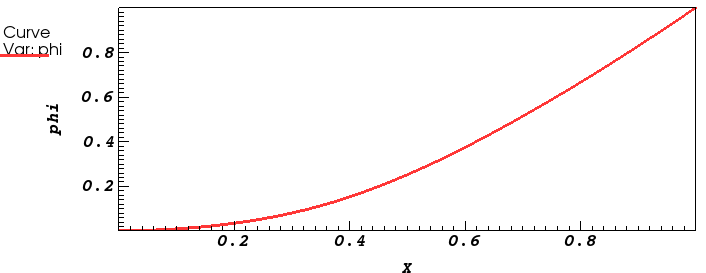
$\Phi(x)$
III
ELECTROMAGNETICS
3D SCL EM parallel plates
Issues with electromagnetic SCL
- Can't specify voltage in EM!
- $\frac{1}{c^2}\frac{d\mathbf{E}}{dt} = \mu_0\mathbf{J}$: Constant $J_\mathrm{SCL}$ means $E$ keeps increasing! Results in oscillatory solution, "virtual cathode"
Workaround: impose displacement current density $J_\mathrm{D}$, then in steady-state: $J_\mathrm{SCL} = J_\mathrm{D}$
Integrate $E$ across the gap to find $V$ across the gap, compare to $V_\mathrm{SCL} = \left(\frac{9}{4} \frac{J_\mathrm{D}}{\epsilon_0}\right)^{\frac{2}{3}} \left(\frac{m}{2e} \right)^{\frac{1}{3}} L^\frac{4}{3}$
David Smithe's 3D simulation of 1D SCL flow (download it!)
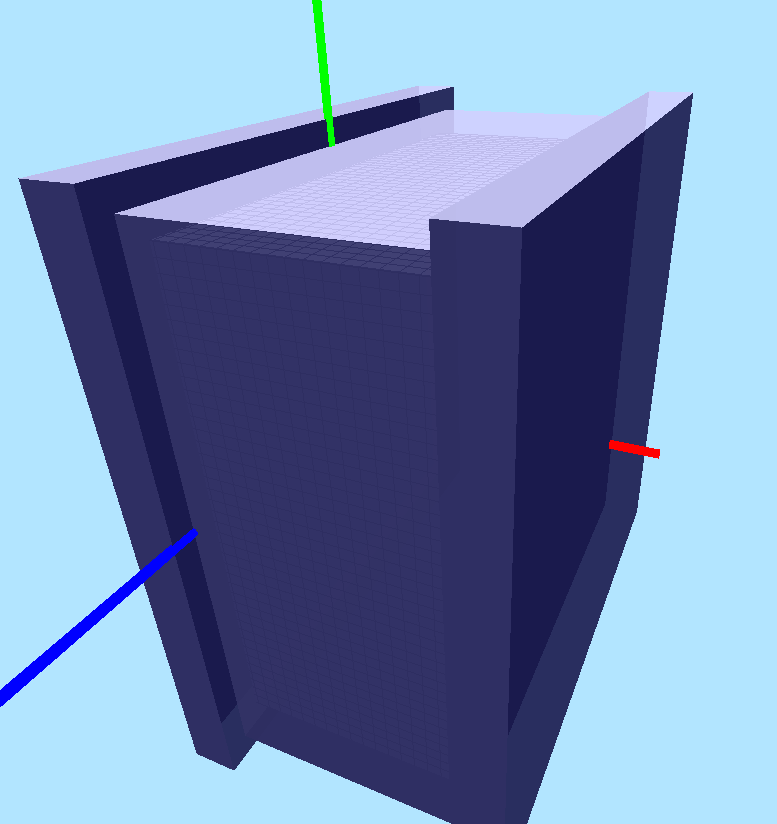
Impose $J_{\mathrm{D},x}$ periodic boundaries in $y$ and $z$
3D SCL EM parallel plates continued
Test Problem: $J_\mathrm{D} = 250\,\frac{\mathrm{A}}{\mathrm{m}^2}$, $L = 10\,\mathrm{cm}$
$V_\mathrm{SCL} = \left(\frac{9}{4} \frac{J_\mathrm{D}}{\epsilon_0}\right)^{\frac{2}{3}} \left(\frac{m}{2e} \right)^{\frac{1}{3}} L^\frac{4}{3} = 10.5\,\mathrm{kV}$
Baseline simulation: funcVelGen with $J_\mathrm{emit} = 1.25J_\mathrm{D}$
$\left[V_\mathrm{SCL}\right]_\mathrm{funcVelGen} = 11.3\,\mathrm{kV}$
Test: childLangmuirVelGen with no emit current specified
$\left[V_\mathrm{SCL}\right]_\mathrm{childLangmuirVelGen} = 10.9\,\mathrm{kV}$
$\left[\color{black}{V_\mathrm{SCL}}\right]_\mathrm{funcVelGen}$
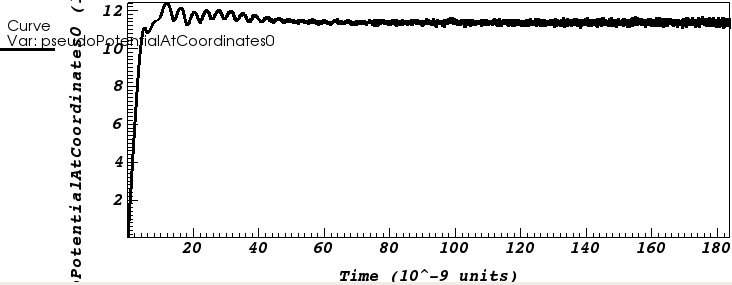
$\left[\color{black}{V_\mathrm{SCL}}\right]_\mathrm{childLangmuirVelGen}$
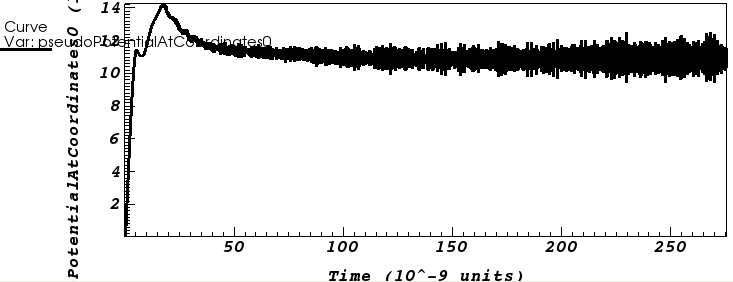
3D SCL EM parallel plates continued
Test Problem: $J_\mathrm{D} = 250\,\frac{\mathrm{A}}{\mathrm{m}^2}$, $L = 10\,\mathrm{cm}$, $A = 0.04\,\mathrm{m}^2$, $J_D = 10 \,\mathrm{A}$
$\left[\color{green}{J_\mathrm{cathode-emit}},\color{blue}{J_\mathrm{cathode-absorb}},\color{red}{J_\mathrm{anode-absorb}}\right]_\mathrm{funcVelGen}$
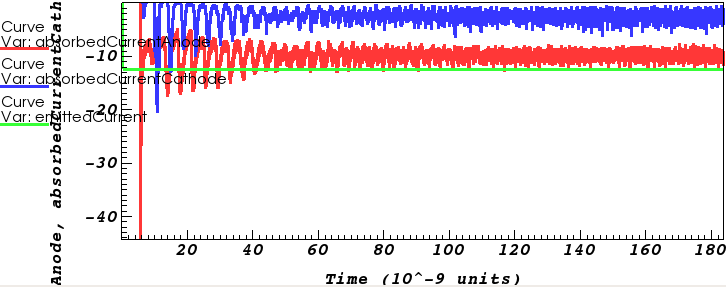
$\left[\color{green}{J_\mathrm{cathode-emit}},\color{blue}{J_\mathrm{cathode-absorb}},\color{red}{J_\mathrm{anode-absorb}}\right]_\mathrm{childLangmuirVelGen}$
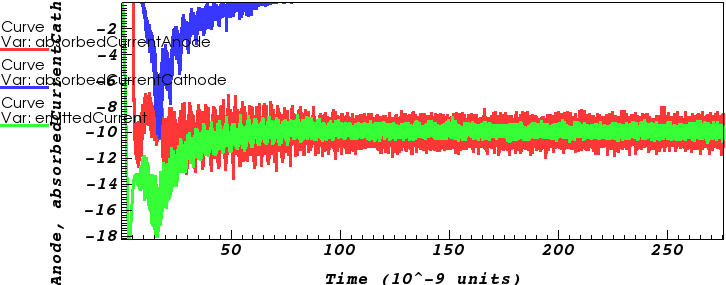
Testing SCL cut-cell emission
Take David Smithe's example, and rotate the plates so that they are not grid-aligned
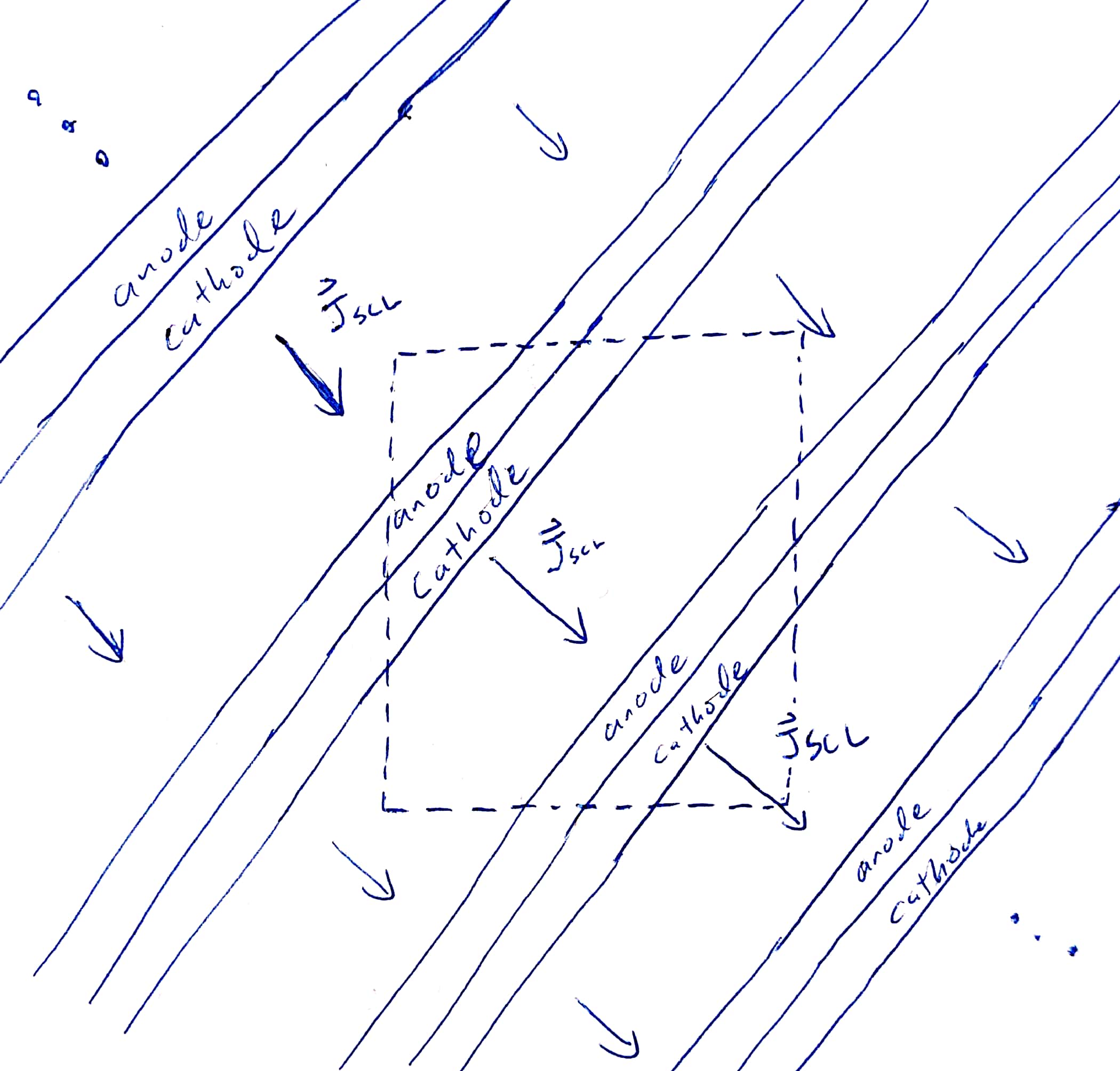
Periodic boundaries in $x$, $y$, and $z$
Testing SCL cut-cell emission
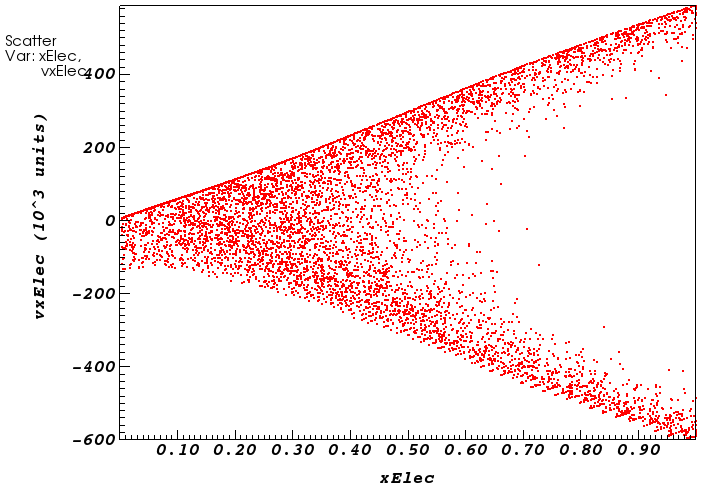
Found strange electron "banding" in both funcVelGen & childLangmuirVelGen
Since $E_\mathrm{normal} \rightarrow 0$, even a small amount of $E_\parallel$ will cause electrons to move parallel to the emitting surface.

IV
TEMPORAL
RESPONSE
Slow Voltage Rise
Voltage rises over a few crossing times
$$\downarrow$$
Similar results to steady-state problem
Fast Voltage Rise
Voltage rises over less than a crossing time
$$\downarrow$$
$J_\mathrm{emit}$ oscillates
Slow Voltage Convergence
Fast Voltage Convergence
V
APPLICATIONS
Magnetically Insulated Line Oscillator (MILO)
Pulsed power microwave device
DC power → electron current → RF power
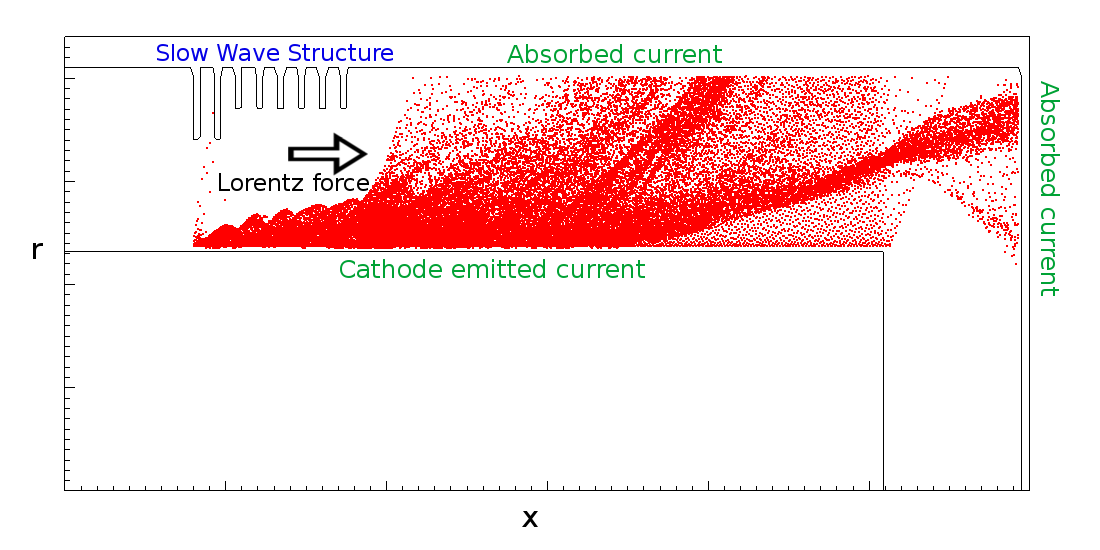
Grid Resolution Depencence:
Slow wave structure at twice the resolution:
Slow wave structure at half the resolution:
Magnetically Insulated Line Oscillator (MILO)
Magnetically Insulated Line Oscillator (MILO)
Magnetically Insulated Line Oscillator (MILO)
Magnetically Insulated Line Oscillator (MILO)
Magnetron
Cathode
Simulation
with the
SCL Emitter
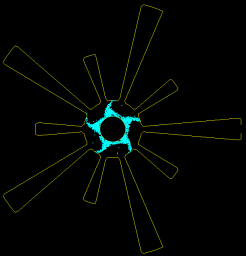
Rising Sun configuration
Plots are zoomed in on the central cathode
Density is oversampled on a $300\times300$ grid and run with a high particle resolution $\sim5\times10^6$ particles.
Magnetron
Cathode
Simulation
with the
Constant current source

Regular Magnetron2D example
VI
FUTURE WORK
Future work
• Currently working on $v_0>0$ that follows $$J_\mathrm{SCL}(v \gt 0) = J_\mathrm{SCL}(v=0)\left[\left(1 + \frac{\frac{1}{2}mv^2}{eV}\right)^\frac{1}{2}\right]^3$$
• Thermal emitter?
Requires numerical solution to find maximum $J_\mathrm{SCL}$ (excluding return current) for $J_\mathrm{SCL}\left(L\mathrm{gap},V_\mathrm{gap},T_\mathrm{surface}\right)$
• Option to make the particle weights more consistent, by specifying macroparticle weight and maximum particles emitted per cell in a step


